이전 글
Exercise 02: PmergeMe
아예 서브젝트에 Ford-johnson 알고리즘을 사용하라고 명시가 되어 있다. 어떻게 적어야할 지 막막한데 일단은 끄적여보겠다.
재귀를 쓰지 않는 코드는 포드 존슨 알고리즘이 아니다..!!
Art of Computer Programming(이하 TAOCP) - Volume 3의 5.3.1, WIKIPEDIA의 Merge-insertion sort를 참고하자.
비교 정렬의 하한
먼저 비교 정렬의 하한을 알아보자. 결론 먼저 보면, 비교 정렬의 하한은 $nlog{n}$ 이다. 즉 어떠한 비교 정렬도 $nlog{n}$ 이상의 효율이 나올 수는 없다. 왜 그럴까?
예를 들어, x, y, z의 세 원소를 정렬한다고 해보자.
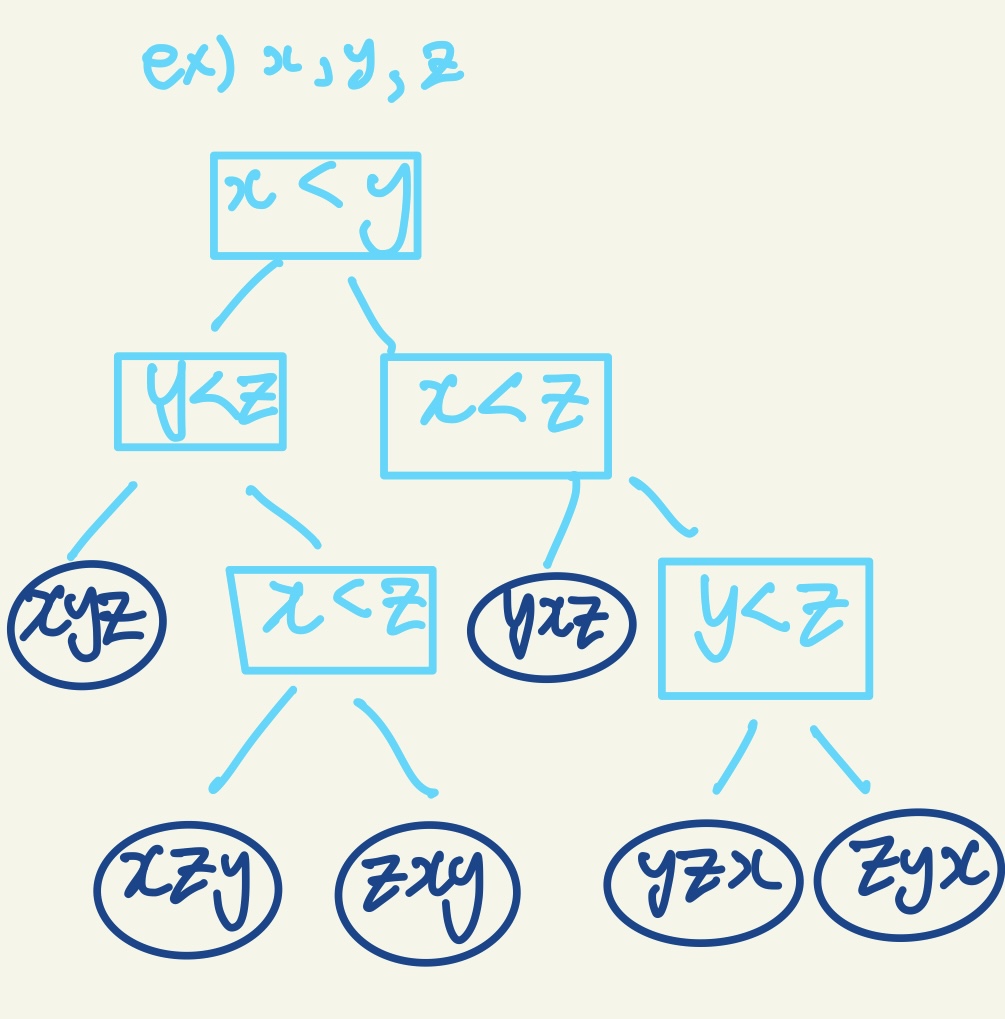
이 떄 결정 트리의 리프(잎, 가장 끝의 노드) 개수는 $3! = 6$ 이다. 즉, 가능한 리프의 최소 개수는 $n!$ 을 따른다.
또한 최대 개수는 결정 트리의 높이(위 예시에서, 높이는 3이다.)를 따른다. 즉, $h$ 를 결정 트리의 높이라 할 때 최대 개수는 $2^h$ 이다.
이에 대해 TAOCP에서는 다음과 같이 말하고 있다.
it follow that there are exactly $n!$ external nodes in a comparison tree that sorts n elements with no redundant comparisons.
. . .
If all the internal nodes of a comparison tree are at levels < k, it is obvious that there can be at most $2^k$ external nodes in the tree.
(TACOP - 5.3.1, p.182)
즉, 리프의 개수를 $L$ 이라 할 때, $L$ 은 다음을 따른다.
이제 양변에 로그를 취하면,
이고, 이는 스털링 근사에 의하여 다음을 따른다.
결론적으로 비교 정렬의 하한은 $nlog{n}$ 이라는 것이 증명된다.
포드 존슨 알고리즘의 로직
TACOP에서는 Binary insertion과 straight two-way merging을 언급하며 두 방법 모두 점근적으로 $nlog{n}$ 에 도달한다고 얘기한다. 다음의 표를 살펴보자.
B(n)은 Binary insertion의 비교 횟수, L(n)은 two-way list merging의 비교 횟수이다.

위 표에서는 모든 $n$ 에 대하여 $B(n) \le L(n)$ 따르는 것으로 보인다. TACOP에서는 여기서 한 가지 의문을 제시한다.
$S(4)=5$ 지만, $S(5)$ 는 7이거나 8이다. 다섯 개의 요소를 7번의 비교만을 통해 정렬할 수 있을까? 여기서 시작된 것이 포드 존슨 알고리즘이다.
다음은 구체적인 방법에 대해서 알아보자. 예를 들어, [11, 7, 5, 3, 20, 22] 의 수열을 정렬 하려 한다.
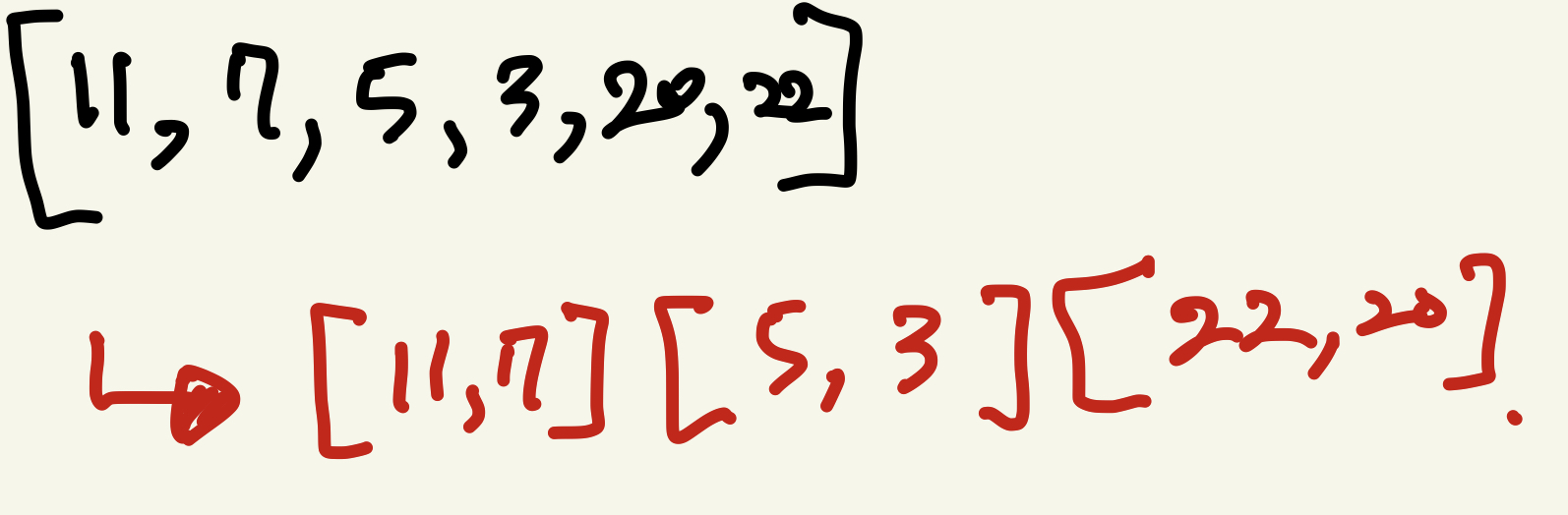
먼저 위와 같이 2개씩 쌍을 지어, 각 쌍을 정렬한다. (만약 홀수이면 남겨놓는 한 개는 작은 숫자들의 끝에 넣는다.) (비교 횟수: 3)
이후, 큰 쌍들을 기준으로 정렬한다. 그러면 다음과 같이 chain구조가 만들어진다.
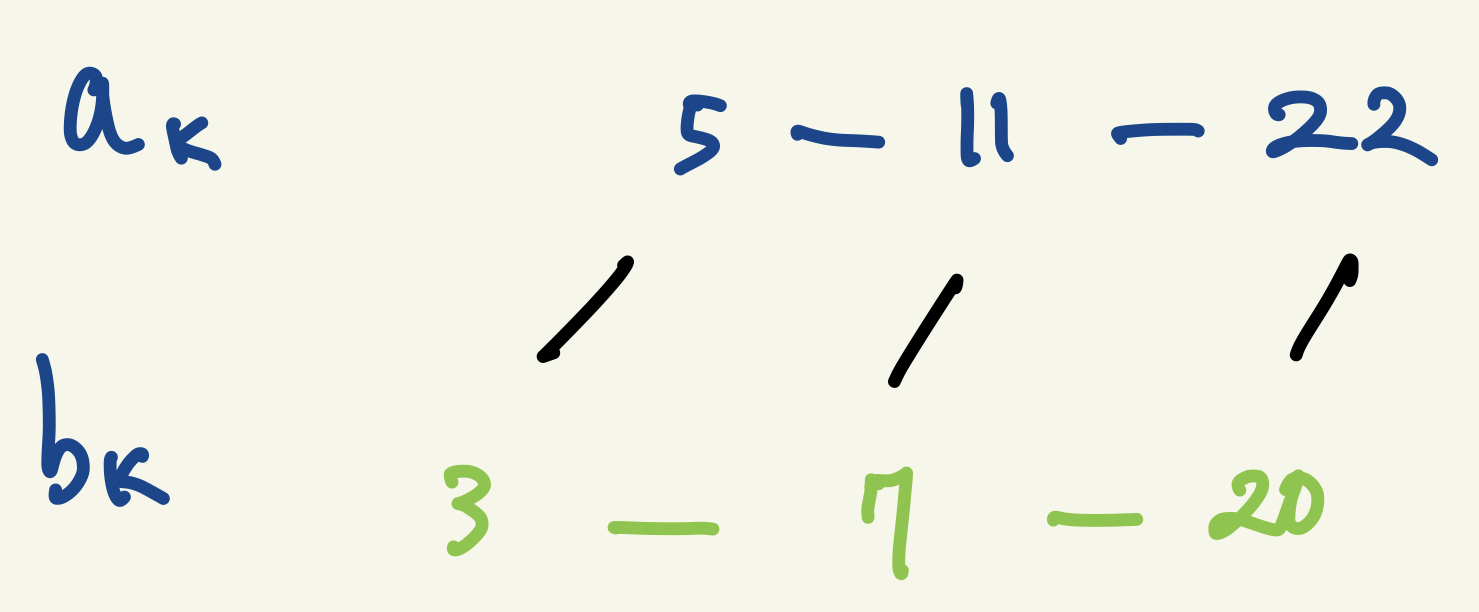
위의 큰 숫자들의 수열($a_k$)을 main-chain이라고 부르자. 각각의 요소는 항상 main-chain이 클 것이다($a_k > b_k$). 이제 작은 숫자들($b_k$)을 각각 main-chain에 이분 탐색을 통해 삽입할 것이다. 단, 삽입하는 $b_k$의 순서는 1, 3, 2, 5, 4, 11, 10, 9, 8 … (Jacobsthal Number) 의 k를 따른다. 왜 그런지는 나중에 설명하겠다.
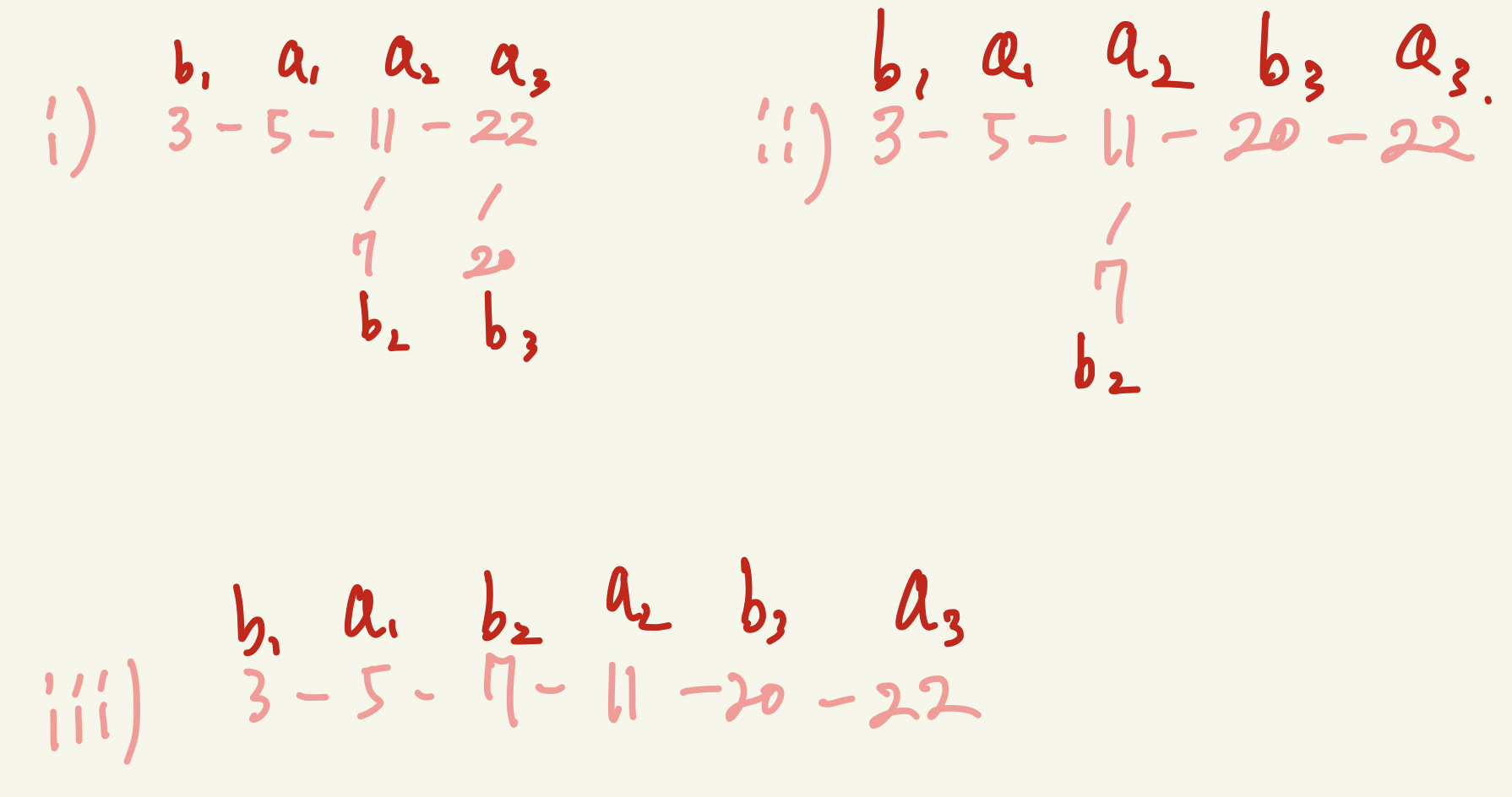
i) $b_1$ 삽입: $b_1$은 $a_1$보다 작으므로 무조건 main-chain의 맨 앞에(main-chain은 정렬되어있기 때문에) 삽입된다. (비교 횟수: 3 + 0)
ii) $b_3$ 삽입: $b_3$은 $a_3$보다 작으므로 이분 탐색의 범위는 $b_1$ ~ $a_2$ 이다. 이분 탐색의 비교 횟수는 2번이다. (비교 횟수: 3 + 0 + 2)
iii) $b_2$ 삽입: $b_2$는 $a_2$보다 작으므로, 이분 탐색의 범위는 $b_1$ ~ $a_1$ 이다. 이분 탐색의 비교 횟수는 2번이다. (비교 횟수: 3 + 0 + 2 + 2)
결과적으로 7번의 비교 횟수를 통해 정렬되었다.
그렇다면 만약 $b_1$ 다음 $b_2$를 먼저 삽입하면 어떻게 될까? 먼저 이분 탐색의 최대 비교 횟수는 다음과 같다.

요소의 개수가 $2^k$의 따라 최대 비교 횟수가 바뀌는 것을 알 수 있다. $B(n)$을 이분 탐색의 최대 횟수라고 해보자.

i) $b_2$ 삽입: $b_2$는 $a_2$보다 작으므로, 이분 탐색의 범위는 $b_1$ ~ $a_1$이며 $B(2) = 2$이다. (비교 횟수: 3 + 0 + 2)
ii) $b_3$ 삽입: $b_3$는 $a_3$보다 작으므로, 이분 탐색의 횟수는 $b_2$가 이미 삽입되어 있으므로 $B(4) = 3$이다. (비교 횟수: 3 + 0 + 2 + 3)
이전과 다르게 비교 횟수가 8번이 나왔다
여기서 우리는, $b_k$를 선택하는 기준이 이분 탐색의 범위가 바뀌지 않는 지점부터 거꾸로 내려온다는 것을 알 수 있다.
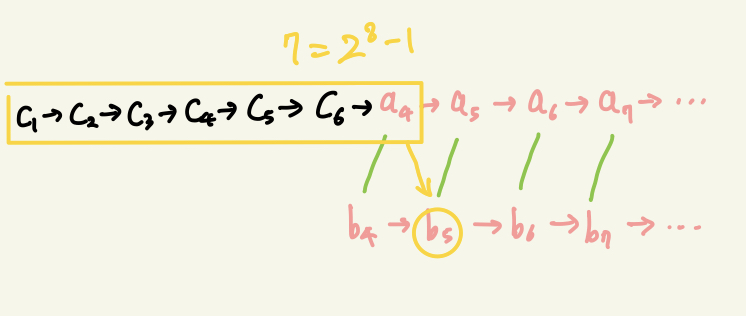
자 그럼, 일반화를 해보자.
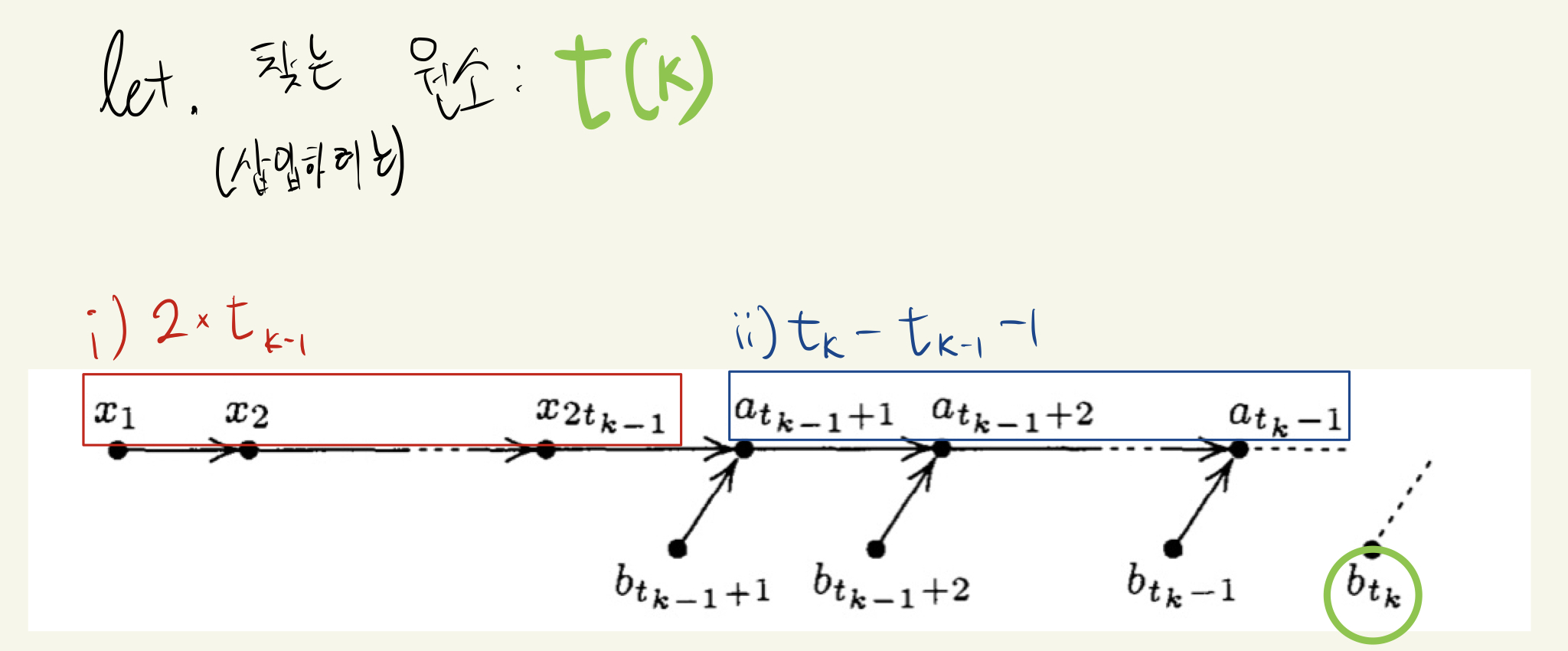
- 1. $x_k$의 수열은 $b_{t_k}$ 이전까지 합쳐진 ($b_k$가 main-chain에 삽입된) $a_{t_{k-1}} + b_{t_{k-1}}$이다. 즉, 개수는 $2t_{k-1}$개이다.
- 2. $a_{t_k}$에서, 1.과정에서 사용된 $a_{t_{k-1}}$을 빼고, 마지막 사용하지 않는 원소(찾으려는 원소는 $b_{t_k}$이니까)인 $a_{t_k}$를 뺀다. 즉, 개수는 $t_k - t_{k-1} - 1$개이다.
- 3. 우리의 최적의 숫자($t_k$)는 이분 탐색의 범위가 바뀌지 않는 숫자, 즉 $(2t_{k-1}) + (t_k - t_{k-1} - 1)$가 $2^k - 1$일 때이다.
- 4.
- 1) $(2t_{k-1}) + (t_k - t_{k-1}) = 2^k$, 즉 $t_{k-1} + t_k = 2^k$
- 2) $t_k + t_{k-1} = 2^k$ => $t_{k-1} + t_{k-2} = 2^{k-1}$, 이제 양변에 2를 곱하자.
- 3) $2t_{k-1} + 2t_{k-2} = 2^k$이고, 이는 다시 1)에 의해 $2t_{k-1} + 2t_{k-2} = t_{k-1} + t_k$ 이다.
- 4) 정리하면, $t_k = t_{k-1} + 2t_{k-2}$ 이다.
- 5. 또한 다음과 같은 식도 도출할 수 있다.
- $t_k = 2^k - t_{k-1} = 2^k - 2^{k-1} + t_{k-2} = 2^k - 2^{k-1} + ... + (-1)^{k}2^0 = \frac{(2^{k+1} + (-1)^k)}{3}$
결론
지금까지의 과정을 정리하면, 결국 포드 존슨 알고리즘의 로직은 다음과 같다.

여기서 주목할 것은, ii)의 마지막 구절이다. “by merge insertion”
즉, main-chain을 정렬하는 과정을 포드 존슨 알고리즘을 통해 재귀적으로 정렬해야한다는 것이다.
이 것이 이 포스트를 시작할 때 재귀를 사용하지 않은 코드는 포드 존슨 알고리즘이 아니라고 한 이유이다.
포드 존슨 알고리즘을 통해 정렬을 하면, 수에 대한 비교 횟수를 $F(n)$이라고 할 때 다음과 같이 정리된다.

예시 겸 실제로 33개의 수를 포드 존슨 알고리즘으로 정렬해보면 다음과 같다.

다음 글에서는 코드의 구현과 관련해서 적어보겠다.